A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in the major segment.


  1. Home
  2. Math
  3. All Questions
Answer:

30°

Step by Step Explanation:
  1. Look at the image below:


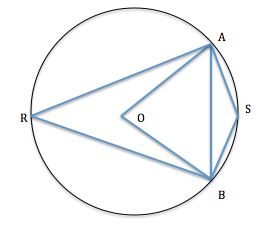
    The chord AB has a length equal to the radius of the circle.
    This means that ΔOAB is an equilateral triangle. (all the sides and angels are equal and each angle measure 60°)
    So, ∠AOB = 60°.
  2. We know that the angle subtended by a chord at the center is twice the angle subtended by the chord at a point in the major segment.
    Consider a point R on the major segment.
    ∠AOB = 2∠ARB.
    Therefore, ∠ARB = 30°

You can reuse this answer
Creative Commons License